Notacja wektora jednostkowego | Wektory i przestrzenie | Algebra liniowa | Khan academy
Kiedy wyjaśniają wymiar W, jest on reprezentowany jako ujemna strona osi X. Dlaczego wymiar W jest ujemny X? Czy to naprawdę nie jest to własny wymiar?

- Spróbuj narysować czterowymiarowy wykres na dwuwymiarowej powierzchni. Oto, co wymyślili (twoje prawo, chociaż nie jest to świetny wykres).
Jak wspomniał @NendoTaka, dość trudno jest narysować obiekt 4d na powierzchni 2d.
Oto jak działa wymiarowość:
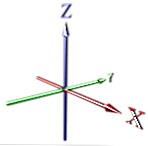
z pojedynczym wymiarem punkt jest wysyłany w nieskończoność, tworząc linię (patrz X)
w 2d dodajemy wymiar prostopadły do tego (patrz X, Y).
Następnie ponownie idziemy prostopadle i rozszerzamy się w górę, aby uzyskać trzeci wymiar (patrz X, Y, Z).
Ponieważ 3d> 2d, nie możemy tak dobrze przedstawić na papierze bez składania papieru lub dodawania na nim większej ilości arkuszy - wszystko to jest naprawdę niepraktyczne do oglądania na ekranie. Zamiast tego używamy perspektywy - tego, jak nasze oczy postrzegają trójwymiarowość. Zazwyczaj kąty tutaj wynoszą ~ 30 stopni.

Wygląda to całkiem nieźle, ponieważ nasze oczy nie widzą w tradycyjnym trójwymiarowym sensie, więc naśladowanie to działa. Ale kiedy chcemy przedstawić czwarty wymiar, nie mamy z czym go porównywać. Musimy znowu iść prostopadle, co jest trudne dla naszych oczu, ponieważ nie mamy zbyt wielu odniesień.
Oto przykładowe przedstawienie czwartego wymiaru:
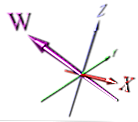
Jest to bardziej poprawny sposób wyświetlania wymiaru, ale nadal opiera się na perspektywie - również nie jest od razu oczywiste, że jest to nowy wymiar na pierwszy rzut oka.
Animatorzy prawdopodobnie zdecydowali się zrobić coś prostego, co byłoby łatwiejsze do animowania. Chociaż, jeśli obrócisz powyższy obraz, wymiary X i W mogą się pokrywać - a to nie byłoby oczywiste na obrazie bez wskaźników strzałek.
Więc tak, są w błędzie - ale nie ma też prostego sposobu na przedstawienie 4 wymiarów na pojedynczym arkuszu papieru
Skoordynuj źródła obrazu i dobrą lekturę
3- 1 Aby być uczciwym, istnieje wiele standardowych sposobów rzutowania 4-wymiarowych obiektów, takich jak teserakty i 3-kule na 3 wymiary (a następnie w zwykły sposób w dół do 2 wymiarów), które znacznie przewyższają te używane w serialu. które mają dodatkową zaletę polegającą na tym, że wyglądają lepiej niż te używane w serialu.
- @senshin och, na pewno, ale myślę, że animatorzy też chcieli coś wyjaśnić, zamiast zadziwiać
- 1 Możesz użyć innych rzeczy niż położenie, aby wskazać, jak daleko wzdłuż osi znajduje się coś, na przykład kolor.






